Дать определение параллельных плоскостей в пространстве. Параллельные плоскости, признак и условия параллельности плоскостей. Взаимно перпендикулярные плоскости

Лекция № 4.

Отклонения формы и расположения поверхностей .

ГОСТ 2.308-79

При анализе точности геометрических параметров деталей различают номинальные и реальные поверхности, профили; номинальное и реальное расположение поверхностей и профилей. Номинальные поверхности, профили и расположения поверхностей определяются номинальными размерами: линейными и угловыми.

Реальные поверхности, профили и расположения поверхностей получаются в результате изготовления. Они всегда имеют отклонения от номинальных.

Допуски формы.

В основу формирования и количественной оценки отклонений формы поверхностей положен принцип прилегающих элементов .

Прилегающий элемент , это элемент соприкасающийся с реальной поверхностью и расположенный вне материала детали, так чтобы расстояние от него в наиболее удалённой точке реальной поверхности в пределах нормируемого участка имело бы минимальное значение.

Прилегающим элементом может быть: прямая, плоскость, окружность, цилиндр и т.п. (Рис. 1, 2).

1 - прилегающий элемент;

2 – реальная поверхность;

L - длина нормируемого участка;

Δ - отклонение формы, определяемое от прилегающего элемента по нормали к поверхности.

Т - допуск формы.

Рис 2. Рис. 1

Поле допуска - область в пространстве, ограниченная двумя эквидистантными поверхностями, отстоящими одна от другой на расстоянии равном допуску Т, который откладывается от прилегающего элемента в тело детали.

Количественное отклонение формы оценивают наибольшим расстоянием от точек реальной поверхности (профиля) до прилегающей поверхности (профиля) по нормали к последней (рис.2). Прилегающими поверхностями служат: рабочие поверхности рабочих плит, интерференционных стекол, лекальных линеек, калибров, контрольных оправок и т.п.

Допуском формы называется наибольшее допускаемое отклонение Δ (рис.2).

Отклонения формы поверхностей.

1. Отклонение от прямолинейности в плоскости – это наибольшее от точек реального профиля до прилегающей прямой. (Рис. 3а).

Рис. 3

Обозначение на чертеже:

Допуск прямолинейности 0,1мм на базовой длине 200мм

2. Допуск плоскостности - это наибольшее допускаемое расстояние () от точек реальной поверхности до прилегающей плоскости в пределах нормированного участка (Рис. 3б).

Обозначение на чертеже:

Допуск плоскостности (не более) 0,02мм на базовой поверхности 200 100 мм.

Методы контроля.

Замер неплоскостности с помощью поворотного плоскомера.
Рис 5а.

Рис 5б. Схема замера неплоскостности.

Контроль в схеме 6б

осуществляется на просвет или

с помощью щупа

(погрешность 1-3мкм)

Рис 6. Схемы замера непрямолинейности.

Контроль плоскостности осуществляют:

Методом «На краску» по количеству пятен в рамке размером 25 25мм

С помощью интерференционных пластин (для доведенных поверхностей до 120мм) (Рис 7).

При наложении пластины с небольшим наклоном на проверяемую поверхность детали прямоугольной формы возникают интерференционные полосы, а на поверхности круглой детали - интерференционные кольца.

При наблюдении в белом свете расстояние между полосами равно в = 0,3мкм (половине длины волны белого света).

Рис. 7.

Неплоскостность оценивается в долях интервала интерференционных полос. По картинке мкм.

мкм

Допуск прямолинейности оси цилиндра 0,01мм (стрелка допуска формы упирается в стрелку размера 20f 7). (Рис 8)

Схема замера

Допуски прямолинейности поверхностей задаются на направляющие; плоскостности - для плоских торцевых поверхностей для обеспечения герметичности (плоскости разъема корпусных деталей); работающих при больших давлениях (торцевые распределители) и т.д.

Допуски прямолинейности осей – для длинных цилиндрических поверхностей (типа штоков), перемещающихся в горизонтальном направлении; цилиндрических направляющих; для деталей, собирающихся с ответными по нескольким поверхностям.

Допуски и отклонения формы цилиндрических поверхностей.

1. Допуск круглости - наиболее допускаемое отклонение от круглости наибольшее расстояние i от точек реальной поверхности до прилегающей окружности.

Поле допуска - область, ограниченная двумя концентрическими окружностями на плоскости перпендикулярной оси поверхности вращения.

Допуск круглости поверхности 0,01мм.

Кругломеры

Рис 9. Схемы замера отклонения от круглости.

Частными видами отклонений от круглости являются овальность и огранка (Рис10).

Овальность Огранка

Для разной огранки индикаторную головку устанавливают под углом (Рис.9б).

2. Допуски цилиндричности - это наибольшее допускаемое отклонение реального профиля от прилегающего цилиндра.

Складывается из отклонения от круглости (замер не менее чем в трех точках) и отклонения от прямолинейности оси.

3. Допуск профиля продольного сечения – это наибольшее допускаемое отклонение профиля или формы реальной поверхности от прилегающего профиля или поверхности (заданных чертежом) в плоскости, проходящей через ось поверхности.

Допуск профиля продольного сечения 0,02мм.
Частные виды отклонения профиля продольного сечения:

Конусность Бочкообразность Седлообразность

Рис 11. Отклонение профиля продольного сечения а, б, в, г и схемы замера д.

Допуски круглости и профиля продольного сечения задаются для обеспечения равномерного зазора в отдельных сечениях и по всей длине детали, например, в подшипниках скольжения, для деталей пары поршень-цилиндр, для золотниковых пар; цилиндричности для поверхностей, требующих полноты контакта деталей (соединяющихся по посадкам с натягом и переходным), а также для деталей большой протяженности типа «штоков».

Допуски расположения

Допуски расположения - это наибольшие допустимые отклонения реального расположения поверхности (профиля), оси, плоскости симметрии от его номинального расположения.

При оценке отклонений расположения отклонения формы (рассматриваемых поверхностей и базовых) должны быть исключены из рассмотрения (Рис 12). При этом реальные поверхности заменяют прилегающими, а за оси, плоскости симметрии принимают оси, плоскости симметрии и центры прилегающих элементов.

Допуски параллельности плоскостей - это наибольшая допускаемая разность наибольшего и наименьшего расстояний между прилегающими плоскостями в пределах нормируемого участка.

Для нормирования и измерения допусков и отклонений расположения вводятся базовые поверхности, оси, плоскости и т.д.Это поверхности, плоскости, оси и т.д., которые определяют положение детали при сборке (работе изделия) и относительно которых задаётся положение рассматриваемых элементов. Базовые элементы на

чертеже обозначаются знаком ; используются большие буквы русского алфавита.

Обозначение баз, разрезов (А-А) не должны дублироваться. Если базой является ось или плоскость симметрии знак ставится на продолжение размерной линии:

Допуск параллельности 0,01мм относительно базовой

поверхности А.

Допуск соосности поверхности в

диаметральном выражении 0,02мм

относительно базовой оси поверхности

В том случае если конструкторская, технологическая (определяющая положение детали при изготовлении) или измерительная (определяющая положение детали при измерении) не совпадают следует выполнить пересчет выполненных измерений.

Измерение отклонений от параллельных плоскостей.

(в двух точках на заданной длине поверхности)

Отклонение определяется как разность показаний головки на заданном интервале друг от друга (головки на «0» выставляются по эталону).

Допуск параллельности оси отверстия относительно базовой плоскости А на длине L.

Рис 14. (Схема замера)

Допуск параллельности осей.

Отклонение от параллельности осей в пространстве - геометрическая сумма отклонений от параллельности проекций осей в двух взаимно перпендикулярных плоскостях. Одна из этих плоскостей является общей плоскостью осей (т.е. проходит через одну ось и точку другой оси). Отклонение от параллельности в общей плоскости - отклонение от параллельности проекций осей на их общую плоскость. Перекос осей - отклонение от проекций осей на плоскость перпендикулярную к общей плоскости осей и проходящую через одну из осей.

Поле допуска - это прямоугольный параллелепипед со сторонами сечения - , боковые грани параллельны базовой оси. Или цилиндр

Рис 15. Схема замера

Допуск параллельности оси отверстия 20H7 относительно оси отверстия 30Н7.

Допуск соосности.

Отклонение от соосности относительно общей оси – это наибольшее расстояние между осью рассматриваемой поверхности вращения и общей осью двух или нескольких поверхностей.

Поле допуска соосности – это область в пространстве, ограниченная цилиндром, диаметр которого равен допуску соосности в диаметральном выражении (Ф = Т ) или удвоенному допуску соосности в радиусном выражении: R=T/2 (рис. 16)

Допуск соосности в радиусном выражении поверхностей и относительно общей оси отверстий А.

Рис 16. Поле допуска соосности и схема замера

(отклонение оси относительно базовой оси А-эксцентриситет); R-радиус первого отверстия (R+e) – расстояние до базовой оси в первом положении замера; (R-e) – расстояние до базовой оси во втором положении после поворота детали или индикатора на 180 градусов.

Индикатор регистрирует разность показаний (R+e)-(R-e)=2e=2 - отклонение от соосности в диаметральном выражении.

Допуск соосности шеек вала в диаметральном выражении 0,02мм (20мкм) относительно общей оси АБ. Валы такого типа устанавливаются (базируются) на опоры качения или скольжения. Базой является ось, проходящая через середины шеек вала (скрытая база).

Рис 17. Схема несоосности шеек вала.

Смещение осей шеек вала приводит к перекосу вала и нарушению эксплуатационных характеристик всего изделия в целом.

Рис 18. Схема замера несоосности шеек вала

Базирование производится на ножевые опоры, которые помещаются в средние сечения шеек валов. При замере отклонение получается в диаметральном выражении D Æ = 2e.

Отклонение от соосности относительно базовой поверхности определяют обычно измерением биения проверяемой поверхности в заданном сечении или крайних сечениях – при вращении детали вокруг базовой поверхности. Результат измерения зависит от некруглости поверхности (которая приблизительно в 4 раза меньше отклонения от соосности).

Рис 19. Схема замера соосности двух отверстий

Точность зависит от точности пригонки оправок к отверстию.

Замер зависимого допуска можно производить с помощью калибра (рис. 20).

Допуск соосности поверхности относительно базовой оси поверхности в диаметральном выражении 0,02мм, допуск зависимый.

Допуск симметричности

Допуск симметричности относительно базовой плоскости – наибольшее допускаемое расстояние между рассматриваемой плоскостью симметрии поверхности и базовой плоскостью симметрии.

Рис 21. Допуски симметричности, схемы замера

Допуск симметричности в радиусном выражении 0,01мм относительно базовой плоскости симметрии А (рис. 21б).

Отклонение DR (в радиусном выражении)равно полуразности расстояний А и Б.

В диаметральном выражении DТ = 2e = А-Б.

Допуски соосности и симметричности назначаются на те поверхности, которые отвечают за точную собираемость и функционирование изделия, где не допускается значительных смещений осей и плоскостей симметрии.

Допуск пересечения осей.

Допуск пересечения осей – наибольшее допускаемое расстояние между рассматриваемой и базовой осями. Он определяется для осей, которые при номинальном расположении должны пересекаться. Допуск задается в диаметральном или радиусном выражении (рис. 22а).

В данной статье будут изучены вопросы параллельности плоскостей. Дадим определение плоскостям, которые параллельны между собой; обозначим признаки и достаточные условия параллельности; рассмотрим теорию на иллюстрациях и практических примерах.

Yandex.RTB R-A-339285-1 Определение 1

Параллельные плоскости – плоскости, не имеющие общих точек.

Чтобы обозначить параллельность применяют такой символ: ∥ . Если заданы две плоскости: α и β , являющиеся параллельными, краткая запись об этом будет выглядеть так: α ‖ β .

На чертеже, как правило, плоскости, параллельные друг другу, отображаются как два равных параллелограмма, имеющих смещение относительно друг друга.

В речи параллельность можно обозначить так: плоскости α и β параллельны, а также – плоскость α параллельна плоскости β или плоскость β параллельна плоскости α .

Параллельность плоскостей: признак и условия параллельности

В процессе решения геометрических задач зачастую возникает вопрос: а параллельны ли заданные плоскости между собой? Для получения ответа на этот вопрос используют признак параллельности, который также является достаточным условием параллельности плоскостей. Запишем его как теорему.

Теорема 1

Плоскости являются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Доказательство этой теоремы приводится в программе геометрии за 10 - 11 класс.

В практике для доказательства параллельности, в том числе, применяют две следующие теоремы.

Теорема 2

Если одна из параллельных плоскостей параллельна третьей плоскости, то другая плоскость или также параллельна этой плоскости, или совпадает с ней.

Теорема 3

Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.

На основе этих теорем и самого признака параллельности доказывается факт параллельности любых двух плоскостей.

Рассмотрим подробнее необходимое и достаточное условие параллельности плоскостей α и β , заданных в прямоугольной системе координат трехмерного пространства.

Допустим, что в некоторой прямоугольной системе координат задана плоскость α, которой соответствует общее уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а также задана плоскость β , которую определяет общее уравнение вида A 2 x + B 2 y + C 2 z + D 2 = 0 .

Теорема 4

Для параллельности заданных плоскостей α и β необходимо и достаточно, чтобы система линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имела решения (являлась несовместной).

Доказательство

Предположим, что заданные плоскости, определяемые уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 являются параллельными, а значит не имеют общих точек. Таким образом, не существует ни одной точки в прямоугольной системе координат трехмерного пространства, координаты которой отвечали бы условиям одновременно обоих уравнений плоскостей, т.е. система A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имеет решения. Если указанная система не имеет решений, тогда не существует ни одной точки в прямоугольной системе координат трехмерного пространства, чьи координаты одновременно отвечали бы условиям обоих уравнений системы. Следовательно, плоскости, заданные уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 не имеют ни одной общей точки, т.е. они параллельны.

Разберем использование необходимого и достаточного условия параллельности плоскостей.

Пример 1

Заданы две плоскости: 2 x + 3 y + z - 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 . Необходимо определить, являются ли они параллельными.

Решение

Запишем систему уравнений из заданных условий:

2 x + 3 y + z - 1 = 0 2 3 x + y + 1 3 z + 4 = 0

Проверим, возможно ли решить полученную систему линейных уравнений.

Ранг матрицы 2 3 1 2 3 1 1 3 равен одному, поскольку миноры второго порядка равны нулю. Ранг матрицы 2 3 1 1 2 3 1 1 3 - 4 равен двум, поскольку минор 2 1 2 3 - 4 отличен от нуля. Таким образом, ранг основной матрицы системы уравнений меньше, чем ранг расширенной матрицы системы.

Совместно с этим, из теоремы Кронекера-Капелли следует: система уравнений 2 x + 3 y + z - 1 = 0 2 3 x + y + 1 3 z + 4 = 0 не имеет решений. Этим фактом доказывается, что плоскости 2 x + 3 y + z - 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 являются параллельными.

Отметим, что, если бы мы применили для решения системы линейных уравнений метод Гаусса, это дало бы тот же результат.

Ответ: заданные плоскости параллельны.

Необходимое и достаточное условие параллельности плоскостей возможно описать по-другому.

Теорема 5

Чтобы две несовпадающие плоскости α и β были параллельны друг другу необходимо и достаточно, чтобы нормальные векторы плоскостей α и β являлись коллинеарными.

Доказательство сформулированного условия базируется на определении нормального вектора плоскости.

Допустим, что n 1 → = (A 1 , B 1 , C 1) и n 2 → = (A 2 , B 2 , C 2) являются нормальными векторами плоскостей α и β соответственно. Запишем условие коллинеарности данных векторов:

n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2 , где t – некое действительное число.

Таким образом, чтобы несовпадающие плоскости α и β с заданными выше нормальными векторами были параллельны, необходимо и достаточно, чтобы имело место действительное число t , для которого верно равенство:

n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2

Пример 2

В прямоугольной системе координат трехмерного пространства заданы плоскости α и β . Плоскость α проходит через точки: A (0 , 1 , 0) , B (- 3 , 1 , 1) , C (- 2 , 2 , - 2) . Плоскость β описывается уравнением x 12 + y 3 2 + z 4 = 1 Необходимо доказать параллельность заданных плоскостей.

Решение

Удостоверимся, что заданные плоскости не совпадают. Действительно, так и есть, поскольку координаты точки A не соответствуют уравнению плоскости β .

Следующим шагом определим координаты нормальных векторов n 1 → и n 2 → , соответствующие плоскостям α и β . Также проверим условие коллинеарности этих векторов.

Вектор n 1 → можно задать, взяв векторное произведение векторов A B → и A C → . Их координаты соответственно: (- 3 , 0 , 1) и (- 2 , 2 , - 2) . Тогда:

n 1 → = A B → × A C → = i → j → k → - 3 0 1 - 2 1 - 2 = - i → - 8 j → - 3 k → ⇔ n 1 → = (- 1 , - 8 , - 3)

Для получения координат нормального вектора плоскости x 12 + y 3 2 + z 4 = 1 приведем это уравнение к общему уравнению плоскости:

x 12 + y 3 2 + z 4 = 1 ⇔ 1 12 x + 2 3 y + 1 4 z - 1 = 0

Таким образом: n 2 → = 1 12 , 2 3 , 1 4 .

Осуществим проверку, выполняется ли условие коллинеарности векторов n 1 → = (- 1 , - 8 , - 3) и n 2 → = 1 12 , 2 3 , 1 4

Так как - 1 = t · 1 12 - 8 = t · 2 3 - 3 = t · 1 4 ⇔ t = - 12 , то векторы n 1 → и n 2 → связаны равенством n 1 → = - 12 · n 2 → , т.е. являются коллинеарными.

Ответ : плоскости α и β не совпадают; их нормальные векторы коллинеарные. Таким образом, плоскости α и β параллельны.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

При оценке отклонений расположения отклонения формы (рассматриваемых поверхностей и базовых) должны быть исключены из рассмотрения (Рис 12). При этом реальные поверхности заменяют прилегающими, а за оси, плоскости симметрии принимают оси, плоскости симметрии и центры прилегающих элементов.

Для нормирования и измерения допусков и отклонений расположения вводятся базовые поверхности, оси, плоскости и т.д.Это поверхности, плоскости, оси и т.д., которые определяют положение детали при сборке (работе изделия) и относительно которых задаётся положение рассматриваемых элементов. Базовые элементы на чертеже обозначаются знаком ; используются большие буквы русского алфавита. Обозначение баз, разрезов (А-А) не должны дублироваться. Если базой является ось или плоскость симметрии знак ставится на продолжение размерной линии:

Допуск параллельности 0,01мм относительно базовой

поверхности А.

Допуск соосности поверхности в

диаметральном выражении 0,02мм

относительно базовой оси поверхности

В том случае если конструкторская , технологическая (определяющая положение детали при изготовлении) или измерительная (определяющая положение детали при измерении) не совпадают следует выполнить пересчет выполненных измерений.

Измерение отклонений от параллельных плоскостей.

(в двух точках на заданной длине поверхности)

Допуск параллельности оси отверстия относительно базовой плоскости А на длине L.

Рис 14. (Схема замера)

Допуск параллельности осей.

Отклонение от параллельности осей в пространстве - геометрическая сумма отклонений от параллельности проекций осей в двух взаимно перпендикулярных плоскостях. Одна из этих плоскостей является общей плоскостью осей (т.е. проходит через одну ось и точку другой оси). Отклонение от параллельности в общей плоскости - отклонение от параллельностипроекций осей на их общую плоскость. Перекос осей - отклонение от проекций осей на плоскость перпендикулярную к общей плоскости осей и проходящую через одну из осей.

Поле допуска - это прямоугольный параллелепипед со сторонами сечения -, боковые грани параллельны базовой оси. Или цилиндр

Рис 15. Схема замера

Допуск параллельности оси отверстия 20H7 относительно оси отверстия 30Н7.

Допуск соосности.

Отклонение от соосности относительно общей оси - это наибольшее расстояние между осью рассматриваемой поверхности вращения и общей осью двух или нескольких поверхностей.

Поле допуска соосности - это область в пространстве, ограниченная цилиндром, диаметр которого равен допуску соосности в диаметральном выражении (Ф = Т ) или удвоенному допуску соосности в радиусном выражении: R=T/2 (рис. 16)

Допуск соосности в радиусном выражении поверхностей и относительно общей оси отверстий А.

Рис 16. Поле допуска соосности и схема замера

(отклонение оси относительно базовой оси А-эксцентриситет); R-радиус первого отверстия (R+e) - расстояние до базовой оси в первом положении замера; (R-e) - расстояние до базовой оси во втором положении после поворота детали или индикатора на 180 градусов.

Индикатор регистрирует разность показаний (R+e)-(R-e)=2e=2 - отклонение от соосности в диаметральном выражении.

Допуск соосности шеек вала в диаметральном выражении 0,02мм (20мкм) относительно общей оси АБ. Валы такого типа устанавливаются (базируются) на опоры качения или скольжения. Базой является ось, проходящая через середины шеек вала (скрытая база).

Рис 17. Схема несоосности шеек вала.

Рис 18. Схема замера несоосности шеек вала

Отклонение от соосности относительно базовой поверхности определяют обычно измерением биения проверяемой поверхности в заданном сечении или крайних сечениях - при вращении детали вокруг базовой поверхности. Результат измерения зависит от некруглости поверхности (которая приблизительно в 4 раза меньше отклонения от соосности).

Рис 19. Схема замера соосности двух отверстий

Точность зависит от точности пригонки оправок к отверстию.

Рис. 20.

Замер зависимого допуска можно производить с помощью калибра (рис. 20).

Допуск симметричности

Допуск симметричности относительно базовой плоскости - наибольшее допускаемое расстояние между рассматриваемой плоскостью симметрии поверхности и базовой плоскостью симметрии.

Рис 21. Допуски симметричности, схемы замера

Допуск симметричности в радиусном выражении 0,01мм относительно базовой плоскости симметрии А (рис. 21б).

Отклонение DR (в радиусном выражении)равно полуразности расстояний А и Б.

В диаметральном выражении DТ = 2e = А-Б.

Допуск пересечения осей.

Допуск пересечения осей - наибольшее допускаемое расстояние между рассматриваемой и базовой осями. Он определяется для осей, которые при номинальном расположении должны пересекаться. Допуск задается в диаметральном или радиусном выражении (рис. 22а).

Рис 22. а)

Допуск пересечения осей отверстий Æ40H7 и Æ50H7 в радиусном выражении 0,02мм (20мкм).

Рис 22. б, в Схема замера отклонения пересечения осей

Оправка помещается в 1 отверстие, замеряется R1 - высота (радиус) над осью .

Оправка помещается в 2 отверстие, замеряется R2 .

Результат замера DR = R1 - R2 получается в радиусном выражении, если радиусы отверстий отличаются, для замера отклонения расположения нужно вычесть действительные значения размеров и (или учесть размеры оправок. Оправка пригоняется по отверстию, контактируют по посадке )

DR = R1 - R2 - ( - ) - отклонение получается в радиусном выражении

Допуск пересечения осей назначается на детали, где несоблюдение этого требования приводит к нарушению эксплуатационных характеристик, например: корпус конического редуктора.

Допуск перпендикулярности

Допуск перпендикулярности поверхности относительно базовой поверхности.

Допуск перпендикулярности боковой поверхности 0,02мм относительно базовой плоскости А. Отклонение перпендикулярности - это отклонение угла между плоскостями от прямого угла (90°), выраженное в линейных единицах D на длине нормируемого участка L .

Рис 23. Схема замера отклонения перпендикулярности

Замер можно проводить несколькими индикаторами выставленными на «0» по эталону.

Допуск перпендикулярности оси отверстия относительно поверхности в диаметральном выражении 0,01 мм на радиусе замера R = 40 мм.

Рис 24. Схема замера отклонения перпендикулярности оси

Допуск перпендикулярности назначается на поверхности, определяющей функционирование изделия. Например: для обеспечения равномерного зазора или плотного прилегания по торцам изделия, перпендикулярности осей и плоскости технологических приспособлений, перпендикулярности направляющих и т.д.

Допуск наклона

Отклонение наклона плоскости - отклонение угла между плоскостью и базой от номинального угла a, выраженное в линейных единицах D на длине нормируемого участка L.

Для замера отклонения используют шаблоны, приспособления.

Позиционный допуск

Позиционный допуск - это наибольшее допускаемое отклонение реального расположения элемента, оси, плоскости симметрии от его номинального положения

Контроль может осуществляться через контроль его отдельных элементов, с помощью измерительных машин, при - калибрами.

Позиционный допуск назначается на расположение центров отверстий под крепежные изделия, сфер шатунов и т.д.

Суммарные допуски формы и расположения

Суммарный допуск плоскостности и параллельности

Назначается на плоские поверхности, определяющие положение детали (базирующие) и обеспечивающие плотное прилегание (герметичность).

Суммарный допуск плоскостности и перпендикулярности.

Назначается на плоские боковые поверхности, определяющие положение детали (базирующие) и обеспечивающие плотное прилегание.

Допуск радиального биения

Допуск радиального биения - это наибольшая допускаемая разность наибольшего и наименьшего расстояний от всех точек реальной поверхности вращения до базовой оси в сечении перпендикулярном базовой оси.

Допуск полного радиального биения.

Рис 26.

Допуск полного радиального биения в пределах нормируемого участка.

радиальное биение является суммой отклонений от круглости и соосности в диаметральном выражении, - суммой отклонений от цилиндричности и соосности.

Допуск радиального и полного радиального биения назначаются на ответственные вращающиеся поверхности, где доминирует требование по соосности деталей, отдельный контроль допусков формы не требуется.Например: выходные концы валов, контактирующие с полумуфтами, участки валов под уплотнения, участки валов, контактирующих по неподвижным посадкам с зазором.

Допуск торцевого биения

Допуск торцевого биения - это наибольшая допускаемая разность наибольшего и наименьшего расстояний от точек на какой-либо окружности торцевой поверхности до плоскости перпендикулярной базовой оси. Отклонение складывается из

отклонений от перпендикулярности и прямолинейности (колебания поверхности окружности).

Допуск полного торцевого биения

Допуск полного торцевого биения - этот наибольшая допустимая разность наибольших и наименьших расстояний от точек всей торцевой поверхности до плоскости перпендикулярной базовой оси.

Допуски торцевого биения задаются на поверхности вращающихся деталей, требующих минимального биения и воздействия на соприкасающиеся с ними детали; например: упорные поверхности для подшипников качения, скольжения, зубчатых колес.

Допуск формы заданного профиля, заданной поверхности

Допуск формы заданного профиля , допуск формы заданной поверхности - это наибольшие отклонения профиля или формы реальной поверхности от прилегающего профиля и поверхности, заданных чертежом.

Допуски задаются на деталях, имеющих криволинейные поверхности типа кулачков, шаблонов; бочкообразные профили и т.д.

Нормирование допусков формы и расположения

Может осуществляться:

· по уровням относительной геометрической точности;

· исходя из худших условий сборки или эксплуатации;

· по результатам расчета размерных цепей.

Уровни относительной геометрической точности.

Согласно ГОСТ 24643-81 для каждого вида допуска формы и расположения установлено 16 степеней точности. Числовые значения допусков при переходе от одной степени точности к другой изменяются с коэффициентом возрастания 1,6.

В зависимости от соотношения между допуском размера и допуском формы и расположения различают 3 уровня относительной геометрической точности:

A - нормальной: задается 60% от допуска T

B - повышенной - задается 40%

С - высокий - 25%

Для цилиндрических поверхностей:

По уровню A » 30% от T

По уровню B » 20% от T

По уровню С » 12,5% от T

Так как допуск формы цилиндрической поверхности ограничивает отклонение радиуса, не всего диаметра.

Например: Æ 45 +0,062 по A:

На чертежах допуск допуска формы и расположения указывают тогда, когда они должны быть меньше допусков размера.

Если же указания нет, то они ограничиваются допуском самого размера.

Обозначения на чертежах

Допуски формы и расположения указываются в прямоугольных рамках; в первой части которой - условный знак, во второй - числовое значения в мм; для допусков расположения, в третьей части указывается база.

Направление стрелки - по нормали к поверхности. Длина замера указывается через знак дроби «/». Если она не указана контроль осуществляется по всей поверхности.

Для допусков расположения, определяющих взаимные расположения поверхностей допускается базовую поверхность не указывать:

Допускается базовую поверхность, ось, указывать без обозначения буквой:

Перед числовым значением допуска следует указывать символ T, Æ, R,сфера,

если поле допуска дано в диаметральном выражении и радиусном, сферой Æ, R применятся для ; (оси отверстия); .

Если знак не указан - допуск задан в диаметральном выражении.

Для допуска симметричности используют знаки T (вместо Æ) или (вместо R).

Зависимый допуск, указывается знаком .

После значения допуска может быть указан символ , а на детали этим символом обозначают участок, относительно которого определяется отклонение.

Нормирование допусков формы и расположения из худших условий сборки .

Рассмотрим деталь, контактирующую одновременно по нескольким поверхностям - шток.

В том случае, если между осями всех трех поверхностей будет большая несоосность, сборка изделия будет затруднена. Возьмем худший для сборки вариант - минимальный зазор в соединении .

Примем за базовую ось- ось соединения .

Тогда смещение оси .

В диаметральном выражении это 0,025мм.

Если базой является ось центровых отверстий, то исходя из аналогичных соображений.

Пример 2.

Рассмотрим ступенчатый вал, контактирующий по двум поверхностям, одна из которых рабочая , ко второй предъявляются только требования собираемости .

Для худших условий сборки деталей: и .

Предположим, что детали втулка и вал идеально соосны: При наличии зазоров и идеально соосных деталей зазоры распределяются равномерно по обе стороны и .

По рисунку видно, что детали соберутся даже, если оси ступеней будут смещены друг относительно друга на величину .

При и , т.е. допустимое смещение осей в радиусном выражении. = e = 0.625мм, или = 2е = 0,125мм - в диаметральном выражении.

Пример 3.

Рассмотрим болтовое соединение деталей, когда образуются зазоры между каждой из соединяемых деталей и болтом (тип А), при этом зазоры расположены в противоположные стороны. Ось отверстия в 1 детали смещена от оси болта на влево, а ось детали 2 на вправо.

Отверстия под крепёжные детали выполняются с полями допусков Н12 или Н14 по ГОСТ 11284-75. Например, под М10 можно использовать отверстия (для точных соединений) и мм (для неответственных соединений). При линейный зазор Смещение осей в диаметральном выражении величина позиционного допуска = 0,5мм, т.е. равна т.к. =.

Пример 4.

Рассмотрим винтовое соединение деталей, когда зазор образуется только между одной из деталей и винтом: (тип Б)

В практике вводят коэффициенты запаса точности: к

Где к = 0,8…1, если сборка осуществляется без регулировки положения деталей;

к = 0,6…0,8 (для шпилек к=0,4)- при регулировке.

Пример 5.

Контактируют две плоские прецизионные торцевые поверхности, S=0.005мм. Требуется пронормировать допуск плоскостности. При наличии торцевых зазоров вследствие неплоскостности (наклоны деталей выбраны с помощью пружин) возникают утечки рабочей жидкости или газа, что снижает объемный КПД машин.

Величину отклонения для каждой из деталей определяем как половину =. Можно округлить до целых величин =0,003мм, т.к. вероятность худших сочетаний довольно незначительна.

Нормирование допусков расположения из расчета размерных цепей.

Пример 6.

Требуется пронормировать допуск соосности установочной оси 1 технологического приспособления, для которого задан допуск всего приспособления = 0,01.

Примечание: допуск всего приспособления не должен превышать 0,3…0,5 допуска изделия.

Рассмотрим факторы, влияющие на соосность всего приспособления в целом:

Несоосность поверхностей детали 1;

Максимальный зазор в соединении деталей 1 и 2;

Несоосность отверстия во 2 детали и базовой (крепление в станок) поверхностью .

Т.к. цепь размеров малозвенная (3 звена) используется для расчёта метод полной взаимозаменяемости; по которому допуск замыкающего звена равняется сумме допусков составляющих звеньев.

Допуск соосности всего приспособления равняется

Для исключения влияния при соединении 1 и 2 деталей следует взять переходную посадку или с натягом.

Если принять , то

Величина достигается на операции тонкой шлифовки. Если приспособление имеет небольшие габариты, то можно обеспечить обработкой в сборе.

Пример 7.

Постановка размеров лесенкой и цепочкой для отверстий под крепежные детали.

Если размеры вытянуты под одну линию - выполнена простановка цепочкой.

TL D 1 = TL 1 + TL 2

TL D 2 = TL 2 + TL 3

TL D 3 = TL 3 + TL 4 , т.е.

На точность замыкающего звена всегда влияют только 2 звена.

Если TL 1 = TL 2 =

Для нашего примера TL 1 = TL 2 = 0,5 (±0,25мм)

Такая простановка позволяет увеличивать допуски составляющих звеньев, снижать трудоемкость обработки.

Пример 9.

Расчет величины зависимого допуска.

Если для примера 2 указаны , то это означает, что допуск соосности 0,125мм, определенный для худших условий сборки может быть увеличен, если зазоры, образующиеся в соединении больше минимальных.

Например, при изготовлении детали получились размеры -39,95мм;- 59,85мм, возникают дополнительные зазоры S доп1 = d 1max - d 1изг = 39,975 - 39,95 = 0,025мм, и S доп2 = d 2max - d 2изг = 59,9 - 59,85 = 0,05мм, оси дополнительно могут быть смещены друг относительно друга на e доп =e 1доп +e 2доп =(в диаметральном выражении на S 1доп + S 2доп = 0,075мм).

Несоосность в диаметральном выражении с учетом дополнительных зазоров будет равняться: = 0,125 + S доп1 + S доп2 = 0,125 + 0,075 = 0,2мм.

Пример 10.

Требуется определить зависимый допуск соосности для детали втулки.

Условное обозначение: допуск соосности отверстия Æ40H7 относительно базовой оси Æ60p6, допуск зависимый только от размеров отверстия.

Примечание: зависимостьуказывается только на те поверхности, где образуются дополнительные зазоры в посадках, для поверхностей, соединяемых по посадкам с натягом или переходным - дополнительные уводы осей исключены.

При изготовлении получились размеры: Æ40,02 и Æ60,04

Т зав = 0,025 + S 1доп = 0,025 + (D изг1 - D min1) =0,025 + (40,02 - 40) = 0,045мм (в диаметральном выражении)

Пример 11.

Определить величину межцентрового расстояния для детали, если размеры отверстий после изготовления равны: D 1изг = 10,55мм; D 2изг = 10,6мм.

Для первого отверстия

Т зав1 = 0,5 + (D 1изг - D 1min) = 0,5 + (10,55 - 10,5) = 0,55мм или ±0,275мм

Для второго отверстия

Т зав2 = 0,5 + (D 2изг - D 2min) = 0,5 + (10,6 - 10,5) = 0,6мм или ±0,3мм

Отклонения на межцентровом расстоянии.

На этом уроке мы дадим определение параллельных плоскостей и вспомним аксиому о пересечении двух плоскостей. Далее мы докажем теорему - признак параллельности плоскостей и, опираясь на нее, решим несколько задач на параллельность плоскостей.

Тема: Параллельность прямых и плоскостей

Урок: Параллельные плоскости

На этом уроке мы дадим определение параллельных плоскостей и вспомним аксиому о пересечении двух плоскостей.

Определение. Две плоскости называются параллельными, если они не пересекаются.

Обозначение : .

Иллюстрация параллельных плоскостей (Рис. 1.)

1. Какие плоскости называются параллельными?

2. Могут ли быть параллельными плоскости, проходящие через непараллельные прямые?

3. Каким может быть взаимное расположение двух прямых, каждая из которых лежит в одной из двух различных параллельных плоскостей?

4. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. - 5-е издание, исправленное и дополненное - М.: Мнемозина, 2008. - 288 с.: ил.

Задания 1, 2, 5 стр. 29

Положение плоскости в пространстве определяется:

тремя точками, не лежащими на одной прямой;
прямой и точкой, взятой вне прямой;
двумя пересекающимися прямыми;
двумя параллельными прямыми;
плоской фигурой.

В соответствии с этим на эпюре плоскость может быть задана:

проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
проекциями точки и прямой (Рисунок 3.1,б);
проекциями двух пересекающихся прямых (Рисунок 3.1,в);
проекциями двух параллельных прямых (Рисунок 3.1,г);
плоской фигурой (Рисунок 3.1,д);
следами плоскости;
линией наибольшего ската плоскости.

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ 1 , фронтальный – απ 2 и профильный – απ 3 , которые она образует при пересечении с известными плоскостями проекций: горизонтальной π 1 , фронтальной π 2 и профильной π 3 (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

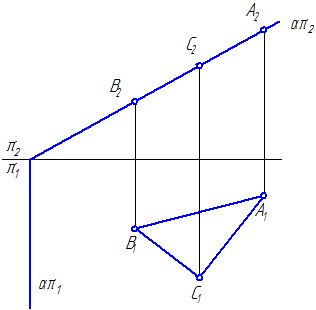
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А , В , С ; линии АС , АВ , ВС ; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций .

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями .

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5).

Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

α = m // n

D ∈ n ⇒ D ∈ α

Рисунок 3.6 – Принадлежность прямой плоскости

Упражнение

Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С .


а	б

Рисунок 3.7 – Решение задачи

Решение :

ABCD – плоский четырехугольник, задающий плоскость.
Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
Согласно признаку пересекающихся прямых, построим горизонтальную проекцию точки пересечения этих прямых — K по её известной фронтальной проекции: A 2 C 2 ∩ B 2 D 2 =K 2 .
Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD : на проекции диагонали B 1 D 1 строим К 1 .
Через А 1 К 1 проводим проекцию диагонали А 1 С 1 .
Точку С 1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А 1 К 1 .

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π 1) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π 2) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π 3) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN .

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π 1 . (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Решение :

Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ 1 (горизонтальный след плоскости);
Точка К должна принадлежать прямой АВ ⇒ К 1 ∈А 1 В 1 и заданной плоскости σ ⇒ К 1 ∈σ 1 , следовательно, К 1 находится в точке пересечения проекций А 1 В 1 и σ 1 ;
Фронтальную проекцию точки К находим посредством линии проекционной связи: К 2 ∈А 2 В 2 .

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.


а	б

Рисунок 3.15 – Пересечение прямой с плоскостью

Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
Если α⊥π 1 , то на плоскость проекций π 1 плоскость α проецируется в прямую (горизонтальный след плоскости απ 1 или α 1), совпадающую с E 1 F 1 ;
Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено );
Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K .

Алгоритм решения задачи (Рисунок 3.15, б):

Через EF проведем вспомогательную плоскость α:

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π 1 или π 2 .

Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций .

Необходимо отдельно определить видимость на каждой плоскости проекций.

Видимость на π 2 (рис. 3.15)

Выберем точки, конкурирующие на π 2 – точки 3 и 4. Пусть точка 3∈ВС∈σ , точка 4∈EF .

Чтобы определить видимость точек на плоскости проекций π 2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π 2 .

Направление взгляда на π 2 показано стрелкой.

По горизонтальным проекциям точек 3 и 4, при взгляде на π 2 , видно, что точка 4 1 располагается ближе к наблюдателю, чем 3 1 .

4 1 ∈E 1 F 1 ⇒ 4∈EF ⇒ на π 2 будет видима точка 4, лежащая на прямой EF , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K

Видимость на π 1

Для определения видимости выберем точки, конкурирующие на π 1 – точки 2 и 5.

Чтобы определить видимость точек на плоскости проекций π 1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π 1 .

Направление взгляда на π 1 показано стрелкой.

По фронтальным проекциям точек 2 и 5, при взгляде на π 1 , видно, что точка 2 2 располагается ближе к наблюдателю, чем 5 2 .

2 1 ∈А 2 В 2 ⇒ 2∈АВ ⇒ на π 1 будет видима точка 2, лежащая на прямой АВ , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.

Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.


а	б

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K .

Построим горизонталь и фронталь в плоскости σ=ΔАВС : A-1 ∈σ; A-1 //π 1 ; С-2 ∈σ; С-2 //π 2 .
Восстановим из точки K перпендикуляр к заданной плоскости: p 1 ⊥h 1 и p 2 ⊥f 2 , или p 1 ⊥απ 1 и p 2 ⊥απ 2

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F ∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

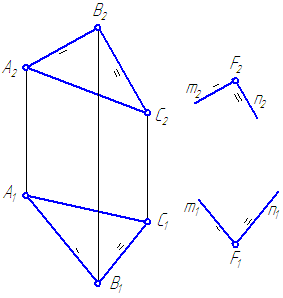
Рисунок 3.17 – Построение плоскости, параллельной заданной

Решение :

В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.

Через точку F проводим прямую m , параллельную, например, АВ .
Через точку F , или же через любую точку, принадлежащую m , проводим прямую n , параллельную, например, ВС , причём m∩ n=F .
β = m ∩n и β//α по определению.

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей.

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Порядок построения линии пересечения плоскостей :

Найти точку пересечения горизонтальных следов — это точка М (её проекции М 1 и М 2 , при этом М 1 =М , т.к. М – точка частного положения, принадлежащая плоскости π 1).
Найти точку пересечения фронтальных следов — это точка N (её проекции N 1 и N 2 , при этом N 2 = N , т.к. N – точка частного положения, принадлежащая плоскости π 2).
Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М 1 N 1 и М 2 N 2 .

М N – линия пересечения плоскостей.

Упражнение

Задана плоскость σ = ΔАВС , плоскость α – горизонтально- проецирующая (α⊥π 1) ⇒α 1 – горизонтальный след плоскости (Рисунок 3.19).

Построить линию пересечения этих плоскостей.

Решение :

Так как плоскость α пересекает стороны АВ и АС треугольника АВС , то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.

Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L , то есть K 1 и L 1 , на пересечении горизонтального следа (α 1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС : А 1 В 1 и A 1 C 1 . После чего посредством линий проекционной связи находим фронтальные проекции этих точек K 2 и L 2 на фронтальных проекциях прямых АВ и АС . Соединим одноимённые проекции: K 1 и L 1 ; K 2 и L 2 . Линия пересечения заданных плоскостей построена.

Алгоритм решения задачи :

KL – линия пересечения ΔАВС и σ (α∩σ = KL ).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Заданы плоскости α = m//n и плоскость β = ΔАВС (Рисунок 3.20).

Построить линию пересечения заданных плоскостей.

Решение :

Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π 2 ; τ⊥π 2 .
Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:

— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7);

— результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).

Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях α и β, то есть на прямой пересечения этих плоскостей;
Аналогично находим точку N , общую для плоскостей α и β.
Соединив точки M и N , построим прямую пересечения плоскостей α и β.

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

Упражнение

Заданы плоскости α = ΔАВС и β = a //b . Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение :

Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π 2 , заключив прямую a во вспомогательную плоскость σ (σ∈a ). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а . Следовательно (1-2)∩а =K .

Точка К принадлежит обеим плоскостям α и β.

Следовательно, точка K , является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β.

Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π 2 (τ∈b ).

Соединив точки K и L , получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π 2 и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Решение .

Проведём перпендикуляр CD к плоскости σ – C 2 D 2 ⊥σ 2 (на основании ).

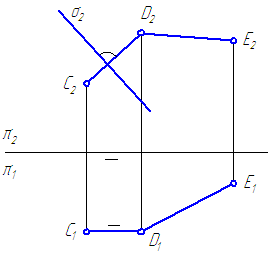
Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C 1 D 1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩ DE задают плоскость τ. Итак, τ⊥σ.

Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Задана плоскость α = ΔАВС и точка K вне плоскости α.

Требуется построить плоскость β⊥α, проходящую через точку K .

Алгоритм решения (Рисунок 3.23):

Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС ;
Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости : если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b 2 ⊥f 2 ; b 1 ⊥h 1 ;
Задаём плоскость β любым способом, например, β = a∩ b , таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m //n (Рисунок 3.24). Известно, что K ∈α.

Постройте фронтальную проекцию точки К .

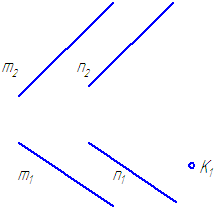
Рисунок 3.24

2. Постройте следы прямой, заданной отрезком CB , и определите квадранты, через которые она проходит (Рисунок 3.25).

Рисунок 3.25

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π 2 , если его диагональ MN //π 2 (Рисунок 3.26).

Рисунок 3.26

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m , исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

Рисунок 3.27

5. Задана плоскость α=a //b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

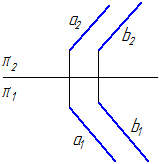
Рисунок 3.28

6. Задана плоскость α=∆АВС и точка D D плоскость β⊥α и β⊥π 1 .

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE //α и DE //π 1 .